CAMPO MAGNÉTICO
F= qv x B
*f: fuerza
*v: velocidad
*B: campo magnético
(Tanto f como v y B son magnitudes vectoriales y el producto vectorial es un producto vectorial que tiene como resultante un vector perpendicular tanto a v como a B)
LA FUERZA RESULTANTE SERÁ =
FUENTES DE CAMPO MAGNETICO
Producido por una carga puntual:
Donde
 . Esta última expresión define un campo vectorial solenoidal:
. Esta última expresión define un campo vectorial solenoidal:Un campo solenoidal es un campo vectorial v cuya divergencia es cero:
Esta condición se satisface si v es derivable de un potencial vector, por ejemplo A, ya que:
Ya que entonces se cumple automáticamente que:
La afirmación contrarrecíproca también es cierta gracias a un teorema de Poincaré, si v es solenoidal en algún punto entonces localmente el campo es expresable como el rotacional de un campo vector.
PROPIEDADES DEL CAMPO MAGNÉTICO
A su vez este potencial vector puede ser relacionado con el vector densidad de corriente mediante la relación:
LEY DE BIOT-SAVART
En el caso de corrientes que circulan por circuitos filiformes (o cerrados), la contribución de un elemento infinitesimal de longitud dL del circuito recorrido por una corriente I crea una contribución elemental de campo magnético, dB, en el punto situado en la posición que apunta el vector Ur a una distancia R respecto de dL , quien apunta en dirección a la corriente I:

*μ0: es la permeabilidad magnética del vacío.
*
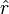 : es un vector unitario.
: es un vector unitario.En el caso de corrientes distribuidas en volúmenes, la contribución de cada elemento de volumen de la distribución, viene dado por:

* 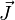 es la densidad de corriente en el elemento de volumen.
es la densidad de corriente en el elemento de volumen.
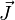 es la densidad de corriente en el elemento de volumen.
es la densidad de corriente en el elemento de volumen.* dv y  es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.
es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.
 es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.
es la posición relativa del punto en el que queremos calcular el campo, respecto del elemento de volumen en cuestión.Se aplica el principio de superposición a través de la expresión:

GENERALIZADA:
*  : es el elemento diferencial de volumen.
: es el elemento diferencial de volumen.
 : es el elemento diferencial de volumen.
: es el elemento diferencial de volumen.* 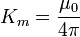 : es la constante magnética.
: es la constante magnética.
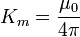 : es la constante magnética.
: es la constante magnética.LEY DE AMPÉRE
Forma integral
Dada una superficie abierta S por la que atraviesa una corriente eléctrica I, y dada la curva C, curva contorno de la superficie S, la forma original de la ley de Ampère para medios materiales es:
donde:
*  : es el campo magnético.
: es el campo magnético.
 : es el campo magnético.
: es el campo magnético.* 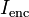 . es la corriente encerrada en la curva C.
. es la corriente encerrada en la curva C.
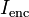 . es la corriente encerrada en la curva C.
. es la corriente encerrada en la curva C.Y se lee: La circulación del campo  a lo largo de la curva C es igual al flujo de la densidad de corriente sobre la superficie abierta S, de la cual C es el contorno.
a lo largo de la curva C es igual al flujo de la densidad de corriente sobre la superficie abierta S, de la cual C es el contorno.
 a lo largo de la curva C es igual al flujo de la densidad de corriente sobre la superficie abierta S, de la cual C es el contorno.
a lo largo de la curva C es igual al flujo de la densidad de corriente sobre la superficie abierta S, de la cual C es el contorno.Definición:
donde:
*  : es la permeabilidad magnética del medio material,
: es la permeabilidad magnética del medio material,
 : es la permeabilidad magnética del medio material,
: es la permeabilidad magnética del medio material,Luego,  es la permeabilidad magnética total.
es la permeabilidad magnética total.
 es la permeabilidad magnética total.
es la permeabilidad magnética total. : es el vector magnetización del material debido al campo magnético.
: es el vector magnetización del material debido al campo magnético. : es la susceptibilidad magnética del material.
: es la susceptibilidad magnética del material.Un caso particular de interés es cuando el medio es el vacío ( o sea,
o sea,  ):
):
 o sea,
o sea,  ):
):Forma diferencial
 donde*
donde* : es el operador rotacional.*
: es el operador rotacional.* : es la densidad de corriente que atraviesa el conductor.
: es la densidad de corriente que atraviesa el conductor.
SOLENOIDE
• B=μ ni
*μ : Coeficiente de permeabilidad.
*n : La densidad de espiras del solenoide.
*i : La corriente que circula.

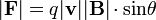
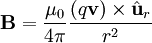








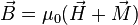
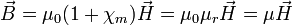
 :
: 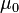 :
: 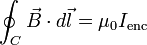
No hay comentarios:
Publicar un comentario